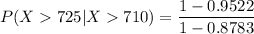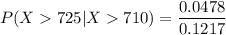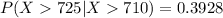Question

Typically, an MBA student who has a GMAT score above 710 is eligible for financial support. Given that a student is eligible for financial support, what is the probability that the student’s GMAT score is higher than 725 ?Typically, an MBA student who has a GMAT score above 710 is eligible for financial support. Given that a student is eligible for financial support, what is the probability that the student’s GMAT score is higher than 725 ?

Answer 1

The correct and complete question is shown below;

The random variable X denotes the GMAT scores of MBA students who were accepted to top MBA programs in Fall 2012. Assume that is normally distributed with a mean
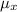`\mu_x` = 675 and a standard deviation
`\sigma_x = 30`

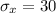
Typically, an MBA student who has a GMAT score above 710 is eligible for financial support. Given that a student is eligible for financial support, what is the probability that the student’s GMAT score is higher than 725?

Answer:

The probability that the student's GMAT score is higher than 725 = 0.3928

Explanation:

From the given information:

Let X be the random variable that follows a normal distribution;

Then;

`X \sim N( \mu_x = 675, \sigma_x = 30)`

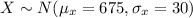
To objective is to determine the probability that
`P(X > 725 | X > 710)`

`P(X > 725 | X > 710)= (P(X > 725 \cap X > 710 ))/(P(X > 725))`

`(P(X > 725 ))/(P(X > 710))=(1 - P(X < 725) )/(1- P(X < 710))`

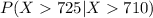
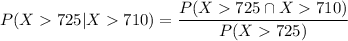
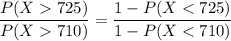
By using the EXCEL FORMULA:

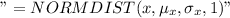
P(X< 725) =

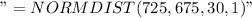
P(X< 725) = 0.9522

P(X< 710) =

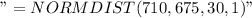
P(X< 710) =0.8783

`P(X > 725 | X > 710)=(1 - 0.9522)/(1- 0.8783)`

`P(X > 725 | X > 710)=(0.0478)/(0.1217)`

`P(X > 725 | X > 710)=0.3928`