Question

Points B and B' have symmetry with respect to P. Find the coordinates of P when B is (2, 8) and B' is (2, 2). A. (2, 5) B. (0, 5) C. (5, 2)

Answer 1

A. (2, 5)

Explanation:

If B and B' have symmetry, then P is a midpoint between those points. We can determinate the location of point P by using the midpoint equation, whose vectorial form is:

`P(x,y) = (1)/(2)\cdot B(x,y)+(1)/(2)\cdot B'(x,y)` (Eq. 1)

If we know that
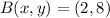`B(x,y) = (2,8)` and
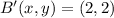`B'(x,y) = (2,2)`, then the location of P is:

`P(x,y) = (1)/(2)\cdot (2,8)+(1)/(2)\cdot (2,2)`

`P(x,y) = (1, 4)+(1,1)`

`P(x,y) = (2, 5)`

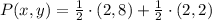
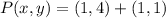
Which corresponds to option A.