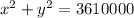Answer:
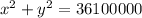
Explanation:
Here it is mentioned that the there are two concentric circles this means that they have the same center.
The center of the circles are the origin
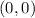 .
.
Radius of the outer circle is
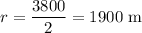
Equation of a circle
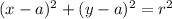
where
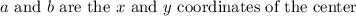
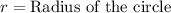
Here the equation will be
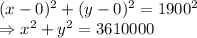
The equation of the outer circle is