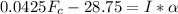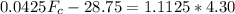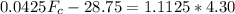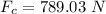Question

During a testing process, a worker in a factory mounts a bicycle wheel on a stationary stand and applies a tangential resistive force of 115 N to the tire's rim. The mass of the wheel is 1.80 kg and, for the purpose of this problem, assume that all of this mass is concentrated on the outside radius of the wheel. The diameter of the wheel is 50.0 cm. A chain passes over a sprocket that has a diameter of 8.50 cm. In order for the wheel to have an angular acceleration of 4.30 rad/s2, what force, in Newtons, must be applied to the chain

Answer 1

The force is
`F_c  =  789.03 \  N`

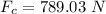
Step-by-step explanation:

From the question we are told that

The tangential resistive force is
`F_t  =   115 \ N`

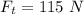
The mass of the wheel is m = 1.80 kg

The diameter of the wheel is
`d =  50.0 cm  = 0.5 \ m`

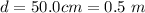
The diameter of the sprocket is
`d_c  =  8.50 \ cm =0.085 \ m`

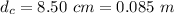
The angular acceleration considered is
`\alpha  =  4.30\ rad/s^2`

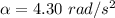
Generally the radius of the wheel is

`r = (d)/(2)`

=>
`r = (0.5)/(2)`

=>
`r = 0.25 \ m`

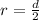
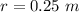
Generally the radius of the sprocket is

`r_c = (d_c)/(2)`

=>
`r_c = (0.085)/(2)`

=>
`r_c = 0.0425 \ m`

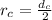
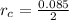
Generally the moment of inertia of the wheel is mathematically represented as

`I  =  m  *  r^2`

=>
`I  =  1.80  *  0.25^2`

=>
`I  = 1.1125 \ kg \cdot m^2`

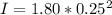
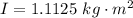
Generally the torque experienced by the wheel due to the forces acting on it is mathematically represented as

`\tau =  F_c *  r_c  -  F_t  * r`

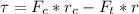
Here
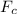`F_c` is the force acting on the sprocket

So

`\tau =  F_c *  0.0425 - 115  * 0.25`

`\tau = 0.0425F_c  -  28.75`

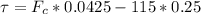
Generally the torques that will cause the wheel to move with
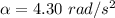`\alpha  =  4.30\ rad/s^2` is mathematically represented as

`\tau  =  I  * \alpha`

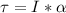
So

`0.0425F_c  -  28.75  =   I  * \alpha`

`0.0425F_c  -  28.75  =   1.1125  *4.30`

`0.0425F_c  -  28.75  =   1.1125  *4.30`

`F_c  =  789.03 \  N`