Answer:
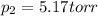
Step-by-step explanation:
Hello.
In this case, by using the Clausius-Clapeyron Equation which allows us to relate the vapor pressure, temperature and heat of vaporization as shown below:
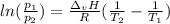
Whereas
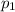 is 760 torr due to the normal conditions. In such a way, for computing the vapor pressure of benzaldehyde at 53.5 °C (326.65 K), we proceed as shown below:
is 760 torr due to the normal conditions. In such a way, for computing the vapor pressure of benzaldehyde at 53.5 °C (326.65 K), we proceed as shown below:
![(p_1)/(p_2) =exp[(48800J/mol)/(8.314(J)/(mol*K))((1)/(326.65K)-(1)/(451.0K) )]\\\\(p_1)/(p_2)=147.0](https://img.qammunity.org/2021/formulas/chemistry/college/lh1bbjg7g68utdewvb80n4cf2c4zs0pv0d.png)
Thus, the vapor pressure at the final T is:
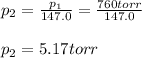
Best regards!