Question

The opening of a tunnel that travels through a mountainside can be modeled by
`y = - \frac {2}{15} (x - 15)(x + 15)`, where x and y are measured in feet. The x-axis represents the ground.

​a. Find the width of the tunnel at ground level.
b. How tall is the tunnel?

Answer 1

(a) 30 feet

(b) 30 feet.

Explanation:

Given that the opening of a tunnel that travels through a mountainside can be modeled by

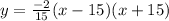`y=(-2)/(15) (x-15)(x+15)`, where x and y are measured in feet.

`\Rightarrow y=(-2)/(15)(x^2-15^2}`

`\Rightarrow y=(-2)/(15){x^2-225}\cdots(i)`

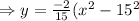
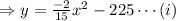
(a) At the ground level,
`y=0`

So, the width of the tunnel at ground level is distance between the extreme point of the tunnel on the grount.

For,
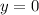`y=0`, the extreme points of the tunnel.

`0=(-2)/(15) (x-15)(x+15)`

`\Rightarrow (x-15)(x+15) =0`

`\Rightarrow x= 15, -15`

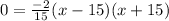
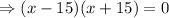
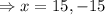
So, the extreme points of the tunnel are,
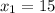`x_1=15` and
`x_2=-15`.

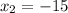Hence, the width of the tunnel at the ground level

`= | x_1 - x_2 |`

`=|15-(-15)|`

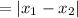
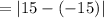
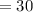`=30` feet.

(b) The maximum height of the tunnel can be determiment by determining the maxima of the given function.

First determining the value of x for which the slope of the graph is zero.

`(dy)/(dx)=0`

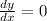
From equation (i),

-2x=0

`\Rightarrow x=0`

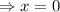
And
`(d^2y)/(dx^2)= -2`

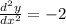
which is always negative, so at x=0 the value of y is maximum.

Again, put x=0 in equation (i), we have

`y=(-2)/(15){0^2-225}`

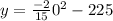
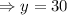`\Rightarrow y=30` feet.

Hence, the tunnel is 30 feet tall.