Question

Runner A is initially 5.8 km west of a flagpole and is running with a constant velocity of 8.6 km/h due east. Runner B is initially 4.9 km east of the flagpole and is running with a constant velocity of 7.1 km/h due west. How far are the runners from the flagpole when their paths cross? Answer in units of km.

Answer 1

Runner A will be 0.05 km from the flagpole, and runner B will be 0.07 km from the flagpole

Step-by-step explanation:

We can find when their paths will cross as follows:

`X_(f) = X_(0) + v_(0)t + (1)/(2)at^(2)`

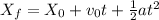
Where:

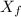`X_(f)` is the final position

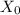`X_(0)` is the initial position

v₀ is the initial speed

t is the time

a is the acceleration = 0 (since they are running with a constant velocity)

When their paths cross we have:

`X_(fA)+X_(fB)=5.8+4.9=10.7 km`

`V_(A)t+V_(B)t=10.7`

`8.6t+7.1t=10.7`

`t = 0.68 h`

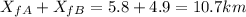
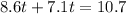
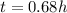
Now we can find the final distance of each runner.

`X_(fA)=V_(A)*0.68`

`X_(fA)=8.6*0.68 km`

`X_(fA)=5.85 km`

`X_(fB)=V_(B)*0.68`

`X_(fB)=7.1*0.68`

`X_(fB)=4.83 km`

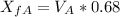
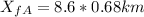
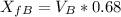
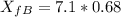
Therefore, runner A will be 0.05 km from the flagpole, and runner B will be 0.07 km from the flagpole.

I hope it helps you!