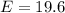Answer:
The value is
Explanation:
From the question we are told that
The mean of Jo cows is
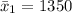
The standard deviation of Jo cow is
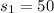
The mean of Val cows is
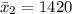
The standard deviation of Val cows is
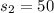
The sample size for both Val and Jo is n = 25
Let assume that the level of significance is

Generally from the normal distribution table the critical value of
 is
is
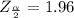
Generally the margin of error is mathematically represented as
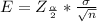
Hence margin of error for Jo is
=>
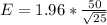
=>