Question

If each unit on the coordinate plane represents one mile, what is the total distance the truck travels on its route?

Answer 1

36.16 miles

Explanation:

A recycling truck begins its weekly route at the recycling plant at point A, as pictured on the coordinate plane below. It travels from point A to point B, then points C, D, and E, respectively, before returning to the recycling plant at point A at the end of the day. The truck’s route is illustrated on the coordinate plane below. If each unit on the coordinate plane represents one mile, what is the total distance the truck travels on its route?

Answer:

The distance between two points X(
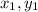`x_1,y_1`) and Y
`(x_2,y_2)` is given as:

`|XY|=√((x_2-x_1)^2+(y_2-y_1)^2)`

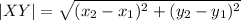
From the image attached, the coordinates of the plane are:

A(-1, -1), B(1, -1), C(5, 2), D(0, 13), E(-5, 2).

The lengths are:

`|AB|=√((1-(-1))^2+(-1-(-1))^2)=2\ units\\ \\|BC|=√((5-1)^2+(2-(-1))^2)=5\ units\\\\|CD|=√((0-5)^2+(13-2)^2)=12.08\ units\\\\|DE|=√((-5-0)^2+(2-13)^2)=12.08\ units\\\\|AE|=√((-5-(-1))^2+(2-(-1))^2)=5\ units`

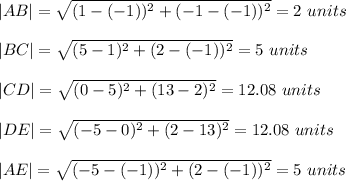
But 1 mile = 1 unit

Total distance = |AB| + |BC| + |CD| + |DE| + |AE| = 2 + 5 + 12.08 + 12.08 + 5 = 36.16 miles