Question

A friend of mine is giving a dinner party. His current wine supply includes bottles of zinfandel, of merlot, and of cabernet (he only drinks red wine), all from different wineries. If he wants to serve bottles of zinfandel and serving order is important, how many ways are there to do this? If bottles of wine are to be randomly selected from the for serving, how many ways are there to do this? If bottles are randomly selected, how many ways are there to obtain two bottles of each variety? If bottles are randomly selected, what is the probability that this results in two bottles of each variety being chosen? If bottles are randomly selected, what is the probability that all of them are the same variety?

Answer 1

Explained below.

Explanation:

The complete question is:

A friend of mine is giving a dinner party. His current wine supply includes 8 bottles of zinfandel, 10 of merlot, and 12 of cabernet (he only drinks red wine), all from different wineries. a. If he wants to serve 3 bottles of zinfandel and serving order is important, how many ways are there to do this? b. If 6 bottles of wine are to be randomly selected from the 30 for serving, how many ways are there to do this? c. If 6 bottles are randomly selected, how many ways are there to obtain two bottles of each variety? d. If 6 bottles are randomly selected, what is the probability that this results in two bottles of each variety being chosen? e. If 6 bottles are randomly selected, what is the probability that all of them are the same variety?

Solution:

In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.

The formula to compute the combinations of k items from n is given by the formula:

`{n\choose k}=(n!)/(k!(n-k)!)`

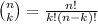
Permutation is the number of ways to select k items from n distinct items in a specific order.

The formula to compute the permutation or arrangement of k items is:

`^(n)P_(k)=(n!)/((n-k)!)`

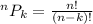
(a)

The number of ways to serve 3 bottles of zinfandel, with a specific order is:

`^(8)P_(3)=(8!)/((8-3)!)=(8*7*6*5!)/(5!)=336`

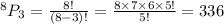
(b)

The number of ways to select 6 bottles from the 30 is:

`{30\choose 6}=(30!)/(6!(30-6)!)=(30!)/(6!* 24!)=593775`

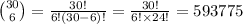
(c)

The number of ways to select two bottles of each variety is:

`{8\choose 2}* {10\choose 2}* {12\choose 2}=(8!)/(2!*6!)* (10!)/(2!*8!)* (12!)/(2!*10!)`

`=(12!)/((2!)^(3)* 6!)\\\\=83160`

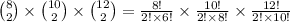
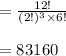
(d)

Compute the probability of selecting two bottles of each variety if 6 bottles are selected:

`P(\text{2 bottles of each})=(83160)/(593775)=0.14`

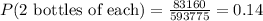
(e)

Compute the probability of selecting the same variety of bottles, if 6 bottles are selected:

`P(\text{Same Variety})=\frac{{8\choose 6}+{10\choose 6}+{12\choose 6}}{{30\choose 6}}`

`=(28+210+924)/(593775)\\\\=0.0019570\\\\\approx 0.002`