Answer:
15 sides
Explanation:
Recall the following about interior and exterior angles of polygons.
Interior angles of polygons:
The formula (n - 2)180 gives the sum of the measures of the interior angles of a polygon of n sides.
If we know the number of sides, we can find the sum of the measures of the angles.
Exterior angles of polygons:
The sum of the measures of the exterior angles of a polygon is 360. If the polygon is a regular polygon of n sides, then the measure of each exterior angle is 360/n.
This problem:
QRSTU is a regular pentagon.
The sum of the measures of the sides of a polygon of n sides is
(n - 2)180
For a pentagon, n = 5, so
(n - 2)180 = (5 - 2)180 = (3)180 = 540
The sum of the measures of the angles of pentagon QRSTU is 540.
Since it's a regular polygon, each angle measures 540/5 = 108.
Angles UQR, R, and S are interior angles of the pentagon, so each one measures 108 degrees.
Now look at polygon VQRS. It is a quadrilateral with sides VQ, QR, RS, and SV. The sum of the measures of the angles of a quadrilateral (4 sides; n = 4) is
(n - 2)180 = (4 - 2)180 = 2(180) = 360
m<VQU = 12 (given)
m<UQR = 108
m<VQR = m<VQU + m<UQR = 108 + 12 = 120
The angles of quadrilateral VQRS are <VQR, <R, <S ,and <TVQ. Their sum is 360.
<VQR + m<R + m<S + m<TVQ = 360
We now substitute the angle values we know and solve for m<TVQ.
120 + 108 + 108 + m<TVQ = 360
m<TVQ = 24
<TVQ is an exterior angle of the large polygon of which PQ, QV and VW are sides.
The sum of the measures of the exterior angles of a polygon, one per vertex, is 360. For a regular polygon, all exterior angles are congruent, and the measure of each exterior angle is the sum of the the measures of the exterior angles divided by the number of sides.
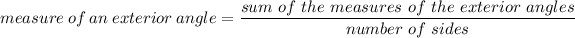
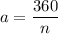
We know that the measure of an exterior angle is 24 deg.
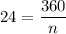
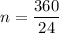

Answer: 15 sides