Answer:
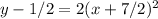
Explanation:
Equation of the Quadratic Function
The vertex form of the quadratic function has the following equation:

Where (h, k) is the vertex of the parabola that results when plotting the function, and a is a coefficient different from zero.
The given function is:
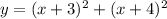
Expanding the squares:
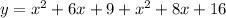
Simplifying:
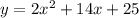
Factoring 2 from the first two terms:

The expression in parentheses must be completed to form the square of a binomial:
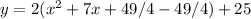
Isolating the square of the binomial:

Operating and Factoring:
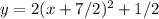
Rearranging:

Comparing with the vertex form:
a=2, h=-7/2, k=1/2