Question

The perimeter of a fence must be no larger than 500 feet in length. The longer side of the fence must be 10 feet more than twice the length of the shorter side. Write and solve and inequality to determine the maximum length of the shorter side of the fence.

Answer 1

The shortest side of the fence can have a maximum length of 80 feet

Explanation:

Inequalities

To solve the problem, we use the following variables:

x=length of the longer side

y=length of the sorter side

The perimeter of a rectangle is calculated as:

P = 2x + 2y

The perimeter of the fence must be no larger than 500 feet. This condition can be written as:

`2x + 2y \le 500`

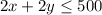
The second condition states the longer side of the fence must be 10 feet more than twice the length of the shorter side.

This can be expressed as:

x = 10 + 2y

Substituting into the inequality:

`2(10 + 2y) + 2y \le 500`

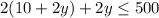
This is the inequality needed to determine the maximum length of the shorter side of the fence.

Operating:

`20 + 4y + 2y \le 500`

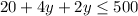
Simplifying:

`20 + 6y \le 500`

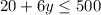
Subtracting 20:

`6y \le 500 - 20`

`6y \le 480`

Solving:

`y \le 480 / 6`

`y \le 80`

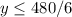
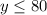
The shortest side of the fence can have a maximum length of 80 feet