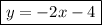Question

Find an

equation for the perpendicular bisector of the line segment whose endpoints
e (-3, -8) and (5,-4).
are

Answer 1

`y=-2x-4`

Explanation:

Perpendicular Bisector

The bisector of a segment defined by points (x1,y1) and (x2,y2) must pass by the midpoint of the segment.

The midpoint (xm,ym) is calculated as follows:

`\displaystyle x_m=(x_1+x_2)/(2)`

`\displaystyle y_m=(y_1+y_2)/(2)`

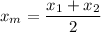
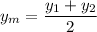
The endpoints of the segment are (-3,-8) and (5,-4), thus the midpoint M is:

`\displaystyle x_m=(-3+5)/(2)=1`

`\displaystyle y_m=(-8-4)/(2)=-6`

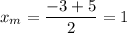
Midpoint: M(1,-6)

Let's find the slope of the given segment. The slope can be calculated with the formula:

`\displaystyle m_1=(y_2-y_1)/(x_2-x_1)`

`\displaystyle m_1=(-4+8)/(5+3)=(1)/(2)`

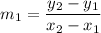
If the bisector is also perpendicular, its slope m2 and the slope of the segment m1 must comply:

`m_1.m_2=-1`

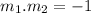
Solving for m2:

`\displaystyle m_2=-(1)/(m_1)=-(1)/((1)/(2))=-2`

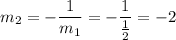
Once we have the slope -2 and the point through which our line must pass (1,-6), we compute the equation in its point-slope form:

`y-y_o=m(x-x_o)`

`y-(-6)=-2(x-1)`

Operating

`y+6=-2(x-1)`

`y+6=-2x+2`

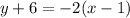
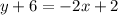
Rearranging

`\boxed{y=-2x-4}`