Answer:
The two numbers are 4 and 6
Explanation:
Suppose we have:
x=The smallest even integer
x+2=Next even integer
Recall even numbers occur every other integer.
The condition of the problem states the square of the smaller integer is 10 more than the longer integer:
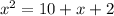
Rearranging and simplifying:
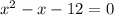
Factoring:
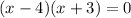
We have two solutions:
x=4, x=-3
Since the integers must be positive:
x=4
Next even integer= x+2=6
The two numbers are 4 and 6