Answer:
Explanation:
Point F is plotted at (5, 4)
Translate ΔABC so that point B maps to point G.
B(1, -1) → G(0, 3)
Rule for the translation,
(x, y) → [x - 1, y + 4]
By this rule,
Point C will map the point,
C(-1, -2) → C'[(-1 - 1), (-2 + 4)]
→ C'(-2, 2)
A(-4, 0) → A'[(-4 - 1), (0 + 4)]
→ A'(-5, 4)
Now reflect these points across y-axis.
Rule for the reflection across y-axis,
(x, y) → (-x, y)
Points after reflection will be,
A'(-5, 4) → F(5, 4)
B'(0, 3) → G(0, 3)
C'(-2, 2) → H(2, 2)
Distance formula,
d =
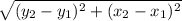
AB =
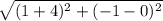 =
=
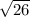
BC =
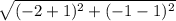 =
=
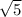
CA =
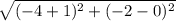 =
=
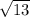
FG =

GH =
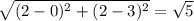
HF =
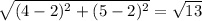
AB ≅ FG, BC ≅ GH, CA ≅ HF
By the SSS property Triangle congruence theorem, ΔABC ≅ ΔFGH