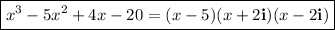Question

What is the complete factorization of the polynomial function over the set of complex numbers?

f(x)=x3−5x2+4x−20



Enter your answer in the box.

Answer 1

`x^3-5x^2+4x-20=(x-5)(x+2\mathbf{i})(x-2\mathbf{i})`

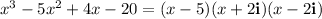
Explanation:

Factorization of polynomials

Factor:

`f(x)=x^3-5x^2+4x-20`

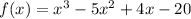
There are several techniques to factor polynomials. We'll use algebraic manipulation and common factor:

Separate in groups:

`(x^3-5x^2)+(4x-20)`

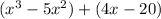
Factor out 4 from 4x-20:

`=(x^3-5x^2)+4(x-5)`

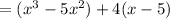
Factor out
`x^2` from
`x^3-5x^2`

`=x^2(x-5)+4(x-5)`

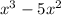
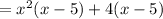
Factor out x-5:

`=(x-5)(x^2+4)`

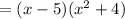
The roots of

`x^2+4=0`

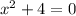
Are two complex numbers:

`x=2\mathbf{i}, x=-2\mathbf{i}`

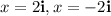
The complete factorization is:

`\boxed{x^3-5x^2+4x-20=(x-5)(x+2\mathbf{i})(x-2\mathbf{i})}`