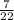Question

What is the probability of picking a blue marble and flipping heads?

Answer 1

7/11

Explanation:

blue = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7 that will be blue.

green = 1 + 1 + 1 + 1 = 4 that will be green.

So it’s going to be 7 + 4 = 11 in total then do

7/11

Is it 7/22

Answer 2

The probability of picking a blue marble and flipping heads is
`(7)/(22)`

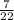
To find the probability of two independent events occurring, you can multiply the probabilities of each event.

Let's denote:

Event A: Picking a blue marble

Event B: Flipping heads

The probability of picking a blue marble (Event A) is the number of favorable outcomes (blue marbles) divided by the total number of outcomes (total marbles).

P(A)=
`(Number of blue marbles)/(Total number of marbles)`

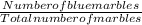
P(A)=
`(7)/(7+4)`

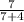
​Now, the probability of flipping heads (Event B) is 1/2, assuming a fair coin.

P(B)=
`(1)/(2)`

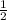
To find the probability of both events happening, you multiply these probabilities:

P(A and B)=P(A)×P(B)

P(Blue marble and Heads)=
`(7 )/(7+ 4) * (1)/(2)`

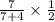
​Now, calculate the product:

P(Blue marble and Heads)=
`(7)/(11) * (1)/(2)`

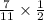
​Multiplying the numerators and denominator

P(Blue marble and Heads)=
`(7* 1)/(11* 2)`

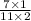
P(Blue marble and Heads)=
`(7)/(22)`

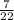
So, the probability of picking a blue marble and flipping heads is
`(7)/(22)`