Answer:
Option (A)
Explanation:
Function to represent the cost of producing 't' tires is,
C(t) = -0.45t² + 12t + 450
Since average rate of change of the function in the interval (a, b) is given by,
Average rate of change =
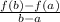
Following this rule,
Average rate of change in the interval (2, 4)
=
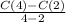
=
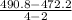
= 9.3
Average rate of change in the interval (46, 48)
=
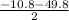
= -30.3
Average rate of change in the interval (12, 14)
=
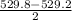
= 0.3
Average rate of change in the interval (22, 24)
=

= --8.7
Average rate of change is greatest in the interval (2, 4)
Option (A) will be the answer.