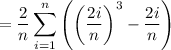Answer:
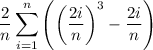
Explanation:
We have the sum:
![\displaystyle \left[\left((2)/(n)\right)}^3-(2)/(n)\right]\left((2)/(n)\right)+...+\left[ \left((2n)/(n)\right)^3-(2n)/(n)\right]\left((2)/(n)\right)](https://img.qammunity.org/2021/formulas/mathematics/college/2dab7mzb7kjmtr5mpfqxnl9nxxwc0hba9d.png)
And we want to find the sigma notation that represents the sum.
Note that the leftmost term is the first term while the rightmost term is the last term.
n is the number of terms. Therefore, (2 / n) will stay constant. Hence, we can factor it out of the series:
![\displaystyle =(2)/(n)\left(\left[\left((2)/(n)\right)^3-(2)/(n)\right]+...+\left[\left((2n)/(n)\right)^3-(2n)/(n)\right]\right)](https://img.qammunity.org/2021/formulas/mathematics/college/apx3v84m1nlw8vc0d9aimz0gkn8jt71q6e.png)
Notice the differences between the first term and the last term. The first term is given by
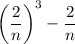 . The last term is given by
. The last term is given by
 . Because at the last term, our initial term i is equal to n, we can replace the extra n with i for our summation.
. Because at the last term, our initial term i is equal to n, we can replace the extra n with i for our summation.
Therefore, we can write the following summation:
![=\displaystyle \sum_(i=1)^(n) (2)/(n)\left(\left[\left((2i)/(n)\right)^3-(2i)/(n)\right]\right)](https://img.qammunity.org/2021/formulas/mathematics/college/v38vug60kugx9889a8lc2t2sywvnzbqdo8.png)
And since (2 / n) is constant: