Question

Martin had 100 trees in his orchard the first year. Each year after that, he

increased the number of trees in his orchard by 10%, rounded to the nearest
whole number. How many trees did he have in his orchard in the sixth year?

Answer 1

• Rate of increase=10%=0.1
• Time=t=6

So trees after 1 year

• 100+10=110

Trees after 2 years

• 110+0.1(110)=121

Trees after 3 years

• 121+0.1(121)
• 133(Whole no)

Trees after 4years

• 133+0.1(133)
• 146

Trees after 5 years

• 146+0.1(146)
• 161

Trees after 6 years

• 161+0.1(161)
• 177trees

Answer 2

177

Explanation:

This scenario can be modeled as an exponential function.

General form of an exponential function:
`y=ab^x`

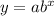
where:

• a is the initial value (y-intercept)
• b is the base (growth/decay factor) in decimal form
• x is the independent variable
• y is the dependent variable

If b > 1 then it is an increasing function

If 0 < b < 1 then it is a decreasing function

If the number of trees increase by 10% each year, then the number of trees each year will be 110% of the number of trees the previous year. Therefore, the growth factor is 110%.

Given:

• a = 100 trees
• b = 110% = 1.10 (in decimal form)
• x = time (in years)
• y = number of trees in the orchard

Substituting the given values into the function:

`\implies y=100(1.10)^x`

(where x is time in years and y is the number of trees in the orchard)

To find how many trees are in the orchard in the 6th year, input x = 6 into the found equation:

`\implies 100(1.10)^6=177.1561=177\: \sf (nearest\:whole\:number)`

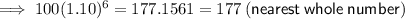
Therefore, Martin had 177 trees in his orchard in the sixth year.