Answer:
177
Explanation:
This scenario can be modeled as an exponential function.
General form of an exponential function:
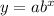
where:
- a is the initial value (y-intercept)
- b is the base (growth/decay factor) in decimal form
- x is the independent variable
- y is the dependent variable
If b > 1 then it is an increasing function
If 0 < b < 1 then it is a decreasing function
If the number of trees increase by 10% each year, then the number of trees each year will be 110% of the number of trees the previous year. Therefore, the growth factor is 110%.
Given:
- a = 100 trees
- b = 110% = 1.10 (in decimal form)
- x = time (in years)
- y = number of trees in the orchard
Substituting the given values into the function:
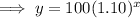
(where x is time in years and y is the number of trees in the orchard)
To find how many trees are in the orchard in the 6th year, input x = 6 into the found equation:
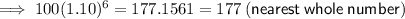
Therefore, Martin had 177 trees in his orchard in the sixth year.