Answer:
See below for answers and explanations
Explanation:
Problem A
The equation of a circle is
 where
where
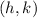 is the center and
is the center and
 is the radius, thus, we need to find
is the radius, thus, we need to find
 using our center and given point, through which we can find our equation:
using our center and given point, through which we can find our equation:
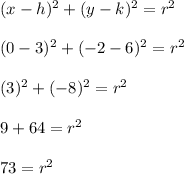
This means that the correct equation is
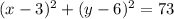
Problem B
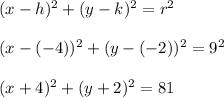
Thus, the correct equation is
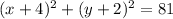
Problem C
Use the distance formula where
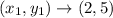 and
and
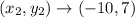 to find the diameter of the circle with the given endpoints:
to find the diameter of the circle with the given endpoints:
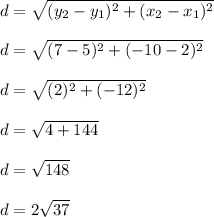
Since the radius is half the diameter, then
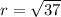 , making
, making
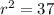 .
.
The midpoint of the two endpoints will give us the center, so the center is
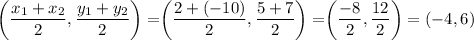
Thus, the correct equation is
