Based on the provided image, the value of y is 39 degrees. This can be determined by using the fact that corresponding angles in congruent triangles are equal.
Polygon BCDE ≅ polygon RSTU
Find the value of x.
Since polygon BCDE ≅ polygon RSTU, corresponding angles are congruent. So, we have the following equations:
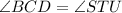
2x + 9 = 2y - 31
Solving for x, we get x = 19°.
Find the value of y.
Since polygon BCDE ≅ polygon RSTU, corresponding sides are congruent. So, we have the following equations:
BD = UT
4w - 7 = 3z + 10
Solving for y, we get y = 39°.
Therefore, the value of each value is 19° and 39°, respectively.