Answers:

========================================================
Step-by-step explanation:
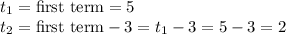
Note we subtract 3 off the previous term (t1) to get the next term (t2). Each new successive term is found this way
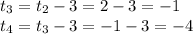
and so on. This process may take a while to reach
There's a shortcut. The nth term of any arithmetic sequence is

We plug in
 and simplify
and simplify
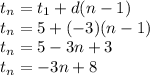
Then we can plug in various positive whole numbers for n to find the corresponding
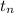 value. For example, plug in n = 2
value. For example, plug in n = 2

which matches with the second term we found earlier. And,
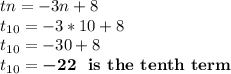
---------------------
The notation
 refers to the sum of the first ten terms
refers to the sum of the first ten terms

We could use either the long way or the shortcut above to find all
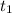 through
through
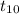 . Then add those values up. Or we can take this shortcut below.
. Then add those values up. Or we can take this shortcut below.
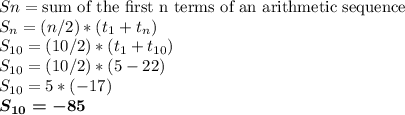
The sum of the first ten terms is -85
-----------------------
As a check for
 , here are the first ten terms:
, here are the first ten terms:
- t1 = 5
- t2 = 2
- t3 = -1
- t4 = -4
- t5 = -7
- t6 = -10
- t7 = -13
- t8 = -16
- t9 = -19
- t10 = -22
Then adding said terms gets us...
5 + 2 + (-1) + (-4) + (-7) + (-10) + (-13) + (-16) + (-19) + (-22) = -85
This confirms that
 is correct.
is correct.