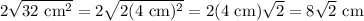Answer:
- 64 cm
- 25.2 m
- 29 1/2 in
- 8√2 cm
- 49.32 ft
Explanation:
The diameter is twice the radius. Each of the given radius values can be multiplied by 2 to find the diameter.
d = 2r
__
1. d = 2(32 cm) = 64 cm
2. d = 2(12.6 m) = 25.2 m
3. d = 2(14 3/4 in) = 29 1/2 in
4. d = 2(√(32 cm²)) = 8√2 cm
5. d = 2(24.66 ft) = 49.32 ft
_____
Additional comment
Variations of this problem ask for the radius, given the diameter. The same relation applies. The radius is half the diameter, so each diameter value would be divided by 2 to find the radius.
__
The simplification of the radical removes the square from under it: