Question

A trebuchet at ground levels throws a boulder with an initial velocity of 25 m/s at 30 degrees.

What was the magnitude of the final velocity of the boulder before it hit the ground?
a
30 m/s
b
10 m/s
C С
25 m/s
ОООООО
d
20 m/s
e
27.5 m/s
12.5 m/s

Answer 1

The correct option is;

C. 25 m/s

Step-by-step explanation:

The initial velocity with which the boulder was thrown = 25 m/s

The path in which the boulder projectile moves = 30°

For projectile motion, we have;

The time it takes the boulder to hit the ground is given by the following equation;

y = y₀ + v₀·sin(θ₀)t -¹/₂·g·t²

Where;

y = The height of the boulder

y₀ = The initial height of the boulder = 0

g = The acceleration due to gravity = 9.81 m/s²

When the boulder touches the ground again, the value of y = 0. therefore, we have;

0 = 0 + 25 × sin(30)t -¹/₂ × 9.81 × t²= 12.5·t - 4.905·t²

From which we have, t = 0 or t ≈ 2.55 s

At t = 2.55 s The vertical velocity = v₀sin(θ₀) - g·t = 25 × 0.5 - 9.81×2.55 = -12.5 m/s

The vertical velocity,
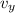`v_y` = -12.5 m/s

The horizontal velocity, vₓ = v₀·cos(θ₀) = 25×cos(30) ≈ 21.65 m/s

The magnitude of the resultant velocity before, the boulder hits the ground is given as follows

`\left | v \right |` = √((vₓ)² + (
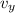`v_y`)²) = √(12.5² + 21.65²) = √625 = 25

The magnitude of the resultant velocity before, the boulder hits the ground is 25 m/c