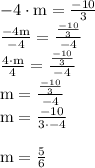Question

Solve the equation: 4(m+2)/4 = 5m-4/3​

Answer 1

m = 5/6

how ❓

When doing math problems, you want to consider...

• First step
• Understand concept
• Why your answer is your answer

To make sure we get to those 3 topics, we will do the long equation.

discuss topics

1. Part 1 is simplifying
2. Part 2 is grouping the left side
3. Part 3 is grouping right side constants
4. Part 4 is isolating m

_______________________________________________________

solve (part 1)

`4\cdot \left(\frac{\mathrm{m}}{4}+(2)/(4)\right)=5\cdot \mathrm{m}+(-4)/(3)\\`

`4\cdot \left(\frac{\mathrm{m}}{4}+(2)/(4)\right)=5\cdot \mathrm{m}+(-4)/(3)`

`4\cdot \left(\frac{\mathrm{m}}{4}+(\left(1\cdot 2\right))/(\left(2\cdot 2\right))\right)=5\cdot \mathrm{m}+(-4)/(3)`

`4\cdot \left(\frac{\mathrm{m}}{4}+(1)/(2)\right)=5\cdot \mathrm{m}+(-4)/(3)`

`\frac{\left(\mathrm{m}\cdot 4\right)}{4}+(\left(1\cdot 4\right))/(2)=5\cdot \mathrm{m}+(-4)/(3)`

`\frac{\left(\mathrm{m}\cdot 4\right)}{4}+(4)/(2)=5\cdot \mathrm{m}+(-4)/(3)`

`\mathrm{m}+(4)/(2)=5\cdot \mathrm{m}+(-4)/(3)`

`\mathrm{m}+(\left(2\cdot 2\right))/(\left(1\cdot 2\right))=5\cdot \mathrm{m}+(-4)/(3)`

`\mathrm{m}+2=5\cdot \mathrm{m}+(-4)/(3)`

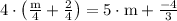
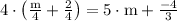
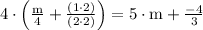
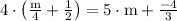
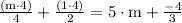
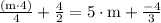
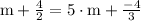
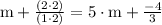
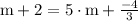
solve (part 2)

`\mathrm{m}+2=5\cdot \mathrm{m}+(-4)/(3)\\\mathrm{m}+2-5\cdot \mathrm{m}=5\mathrm{m}+(-4)/(3)-5\cdot \mathrm{m}\\\mathrm{m}-5\cdot \mathrm{m}+2=5\cdot \mathrm{m}+(-4)/(3)-5\cdot \mathrm{m}\\-4\cdot \mathrm{m}+2=5\cdot \mathrm{m}+(-4)/(3)-5\cdot \mathrm{m}\\-4\cdot \mathrm{m}+2=5\cdot \mathrm{m}-5\cdot \mathrm{m}+(-4)/(3)\\-4\cdot \mathrm{m}+2=(-4)/(3)`

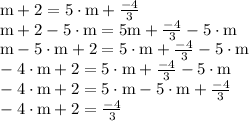
solve (part 3)

`-4\cdot \mathrm{m}+2=(-4)/(3)\\-4\mathrm{m}+2-2=(-4)/(3)-2\\-4\cdot \mathrm{m}=(-4)/(3)-2\\-4\cdot \mathrm{m}=(-4)/(3)+(-6)/(3)\\-4\cdot \mathrm{m}=(-4-6)/(3)\\\\-4\cdot \mathrm{m}=(-10)/(3)`

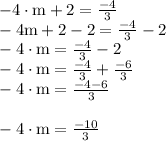
solve (part 4)

`-4\cdot \mathrm{m}=(-10)/(3)\\\frac{-4\mathrm{m}}{-4}=((-10)/(3))/(-4)\\\frac{4\cdot \mathrm{m}}{4}=((-10)/(3))/(-4)\\\mathrm{m}=((-10)/(3))/(-4)\\\mathrm{m}=(-10)/(3\cdot -4)\\\\\mathrm{m}=(5)/(6)`