Question

Please Help! i dont understand

Answer 1

P = 43.3 units

Explanation:

the area (A) of the triangle is calculated as

A =
`(1)/(2)` bh ( b is the base and h the height )

given A = 56 units²

with b =
`(1)/(3)` h

then

`(1)/(2)` bh = 56 ( multiply both sides by 2 to clear the fraction )

bh = 112 , so

`(1)/(3)` h × h = 112 ( multiply both sides by 3 to clear the fraction )

h² = 336 ( take square root of both sides )

h =
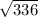`√(336)` ≈ 18.3

then b =
`(1)/(3)` h =
`(1)/(3)` × 18.3 = 6.1

the height h from the vertex to the base bisects the base ( altitude ), that is

`(1)/(2)` b =
`(1)/(2)` × 6.1 = 3.05

this divide the isosceles triangle into 2 right triangles

let the leg of the triangle be x

then using Pythagoras' identity in the right triangle formed

x² = 18.3² + 3.05² = 334.89 + 9.3 = 334.19 ( take square root of both sides )

x =
`√(334.19)` ≈ 18.6

Then perimeter (P) is

P = 2x + b = 2(18.6) + 6.1 = 37.2 + 6.1 = 43.3 units

Answer 2

43.3 units

Explanation:

Base and height of the triangle

`\text{Area of a triangle}=\rm (1)/(2)bh`

where:

• b is the base
• h is the height

Given:

• Area = 56 units²
• 
  `\rm b=(1)/(3)h`

Substitute the given values into the formula and solve for h:

`\begin{aligned}\text{Area of a triangle} & = \rm (1)/(2)bh\\\\\implies \rm 56 & = \rm (1)/(2) \cdot (1)/(3)h \cdot h\\\\\rm 336 & = \rm h^2\\\\\rm h & = \rm 4√(21)\:units \end{aligned}`

Substitute the found value of h into
`\rm b=(1)/(3)h` and solve for b:

`\implies \rm b=(1)/(3)\cdot 4√(21)=(4√(21))/(3)\:units`

Length of one side of the isosceles triangle

`\begin{aligned}\rm side\:length & =\rm \sqrt{\left((b)/(2)\right)^2+h^2}\\\\\ \implies \text{side length}& =\rm \sqrt{\left((4√(21))/(6)\right)^2+(4\sqrt21})^2}\\\\& =\rm \sqrt{(28)/(3)+336}\\\\& =\rm \sqrt{(1036)/(3)}\\\\& = \rm (2√(777))/(3)\:units\end{aligned}`

Total Perimeter

`\begin{aligned}\rm Total\:perimeter & = \rm base + 2\:sides\\\\\implies \text{Total perimeter}& = \rm (4√(21))/(3)+2 \cdot (2√(777))/(3)\\\\& = \rm 43.2763939...\\\\& = \rm 43.3\:units\:(nearest\:tenth)\end{aligned}`