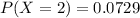Question

In kidney transplantations, compatibility between donor and receiver depends on such factors as blood type and antigens. Suppose that for a randomly selected donor from a large national kidney registry, there is a 10% chance that he or she is compatible with a specific receiver. A sample of size 5 donors are randomly selected from this registry. Find the probability that exactly 2 of the selected donors is compatible.

Answer 1

The probability is
`P(X = 2)= 0.0729`

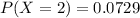
Explanation:

From the question we are told that

The percentage that the donor is compactible is p = 0.10

The sample size is n = 5

Generally the probability that the donor is not compactible is

`q =  1- p`

=>
`q =  1- 0.10`

=>
`q = 0.90`

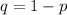
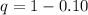
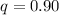
Generally the probability that the exactly 2 of the selected donors is compatible mathematically represented as

`P(X = 2)= \  ^(5)C_2 *  p^2 *  q^(5-2)`

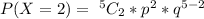
Here C standards for combination

=>
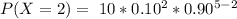
`P(X = 2)= \  10 *  0.10^2 *  0.90 ^(5-2)`

=>
`P(X = 2)= 0.0729`