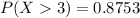Answer:
The probability the earth is saved is
Explanation:
From the question we are told that
The number of missiles lunched by earth is n = 500
The probability that each missile will hit the rocket is p(x) = 0.01
Generally the expected number of missiles that will hit the rocket is
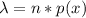

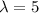
Gnerally the probability that Earth will be saved is mathematically represented as
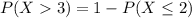
=>

Gnerally the probability distribution function of a Poisson distribution is
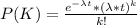
Here t = 1
Hence
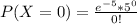
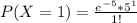
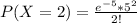
![P(X > 3) = 1 - [ (e^(-5) * 5^0 )/(0!) + (e^(-5) * 5^1 )/(1!) + (e^(-5) * 5^2 )/(2!)]](https://img.qammunity.org/2021/formulas/mathematics/college/kv9jd36xsjirzs3zez1tij3lfqqft25ken.png)
![P(X > 3)= 1 - [ (0.00673 )/(1) + (0.033689)/(1) + (0.168449 )/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/hjyrs9zokctdn46keyp7v1hpkrmv743y78.png)