Question

Blood pressure: High blood pressure has been identified as a risk factor for heart attacks and strokes. The proportion of U.S. adults with high blood pressure is 0.4. A sample of 39 U.S. adults is chosen. Use the TI-84 Plus Calculator as needed. Round the answer to at least four decimal places. Part: 0 / 60 of 6 Parts Complete Part 1 of 6 Is it appropriate to use the normal approximation to find the probability that more than 43% of the people in the sample have high blood pressure? It ▼(Choose one) appropriate to use the normal curve, since =np ▼(Choose one)10 and =n−1p ▼(Choose one) 10.

Answer 1

Yes it appropriate to use the normal approximation to find the probability that more than 43% of the people in the sample have high blood pressure

Explanation:

From the question we are told that

The population proportion is p=0.4

The sample size is n = 39

The sample proportion is
`\^ p = 0.43`

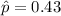
Generally for normal approximation to be used

`np > 10`

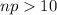
so np = 39 * 0.4 = 15.6 > 10

and
`n(1- p) > 10`

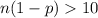
so n(1-p ) = 39(1-0.4) = 23.4 >10

Given that the both condition is meet it mean that it appropriate to use the normal approximation to find the probability that more than 43% of the people in the sample have high blood pressure