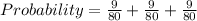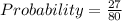Answer:
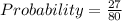
Explanation:
Given
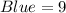
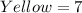
Required
Determine the probability that one of the balls is blue while others is yellow
The order of selection may be any of these three:
Yellow, Yellow, Blue or Yellow, Blue, Yellow or Blue, Yellow, Yellow
Solving Yellow, Yellow, Blue
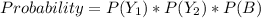
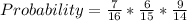
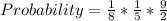
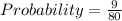
Solving Yellow, Blue, Yellow
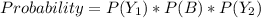
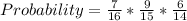
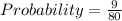
Solving Blue, Yellow, Yellow
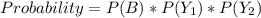
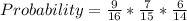
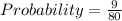
Hence:
The required probability is: