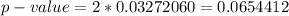Answer:
1 a
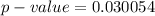
1b

1c
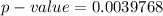
2a
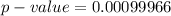
2b

2c
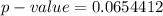
Explanation:
Considering question a
The alternative hypothesis is H1:μ>μ0
The test statistics is z =1.88
Generally from the z-table the probability of z =1.88 for a right tailed test is
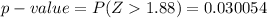
Considering question b
The alternative hypothesis is H1:μ<μ0
The test statistics is z=−2.75
Generally from the z-table the probability of z=−2.75 for a left tailed test is
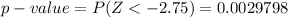
Considering question c
The alternative hypothesis is H1:μ≠μ0
The test statistics is z=2.88
Generally from the z-table the probability of z=2.88 for a right tailed test is
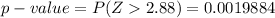
Generally the p-value for the two-tailed test is
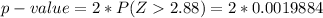
=>
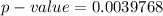
Considering question 2a
The alternative hypothesis is H1:μ>μ0
The sample size is n=16
The test statistic is t = 3.733
Generally the degree of freedom is mathematically represented as
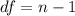
=>
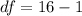
=>
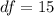
Generally from the t distribution table the probability of t = 3.733 at a degree of freedom of
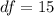 for a right tailed test is
for a right tailed test is
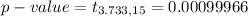
Considering question 2b
The alternative hypothesis is H1:μ<μ0
The degree of freedom is df=23
The test statistic is ,t= −2.500
Generally from the t distribution table the probability of t= −2.500 at a degree of freedom of df=23 for a left tailed test is
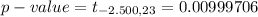
Considering question 2c
The alternative hypothesis is H1:μ≠μ0
The sample size is n= 7
The test statistic is ,t= −2.2500
Generally the degree of freedom is mathematically represented as
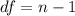
=>
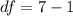
=>

Generally from the t distribution table the probability of t= −2.2500 at a degree of freedom of
 for a left tailed test is
for a left tailed test is
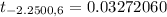
Generally the p-value for t= −2.2500 for a two tailed test is