Question

Estimate the rotor inertia assuming that the rotor is a cylinder of radius 8.98 mm, and length 25 mm, with a material of 100% copper. Explain why the rotor inertia may differ from these assumptions?

Answer 1

The moment of inertia of the rotor is approximately
`1.105* 10^(-6)` kilogram-square meters.

The rotor inertia may differ from these assumption due to differences in the shape of cross section.

Step-by-step explanation:

We assume that rotor can be represented as a solid cylinder of radius
`r`, length
`l`, made of cooper (
`\rho = 8960\,(kg)/(m^(3))`) and whose axis of rotation passes through its center of mass and is parallel to its cross section. By definition of Moment of Inertia and Theorem of Parallel Axes, the moment of inertia of the rotot is:

`I = (1)/(4)\cdot \rho \cdot \left((\pi)/(4) \right) \cdot R^(3)\cdot (3\cdot R^(2)+L^(2))`

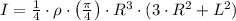
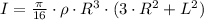`I = (\pi)/(16)\cdot \rho \cdot R^(3)\cdot (3\cdot R^(2)+L^(2))` (Eq. 1)

Where:

`\rho` - Density of copper, measured in kilograms per cubic meter.

`R` - Radius of the rotor, measured in meters.

`L` - Length of the rotor, measured in meters.

`I` - Moment of inertia, measured in kilogram-square meters.

If we know that
`\rho = 8960\,(kg)/(m^(3))`,
`L = 25* 10^(-3)\,m` and
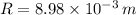`R = 8.98* 10^(-3)\,m`, the estimated moment of inertia of the rotor is:

`I = (\pi)/(16)\cdot \left(8960\,(kg)/(m^(3)) \right)\cdot (8.98* 10^(-3)\,m)^(3)\cdot [3\cdot (8.98* 10^(-3)\,m)^(2)+(25* 10^(-3)\,m)^(2)]`

`I \approx 1.105* 10^(-6)\,kg\cdot m^(2)`

The moment of inertia of the rotor is approximately
`1.105* 10^(-6)` kilogram-square meters.

From D'Alembert's Formula we know that net force of rigid bodies experimenting rotation equals the product of moment of inertia and angular acceleration. In this case, the purpose is minimizing moment of inertia and it is done by modifying the shape of the cross section so that rotor could be aerodynamically more efficient.