Complete Question
An analysis of several polls suggests that 60% of all Florida voters plan to vote for Anderson. A poll of 250 randomly selected Florida voters shows that 144 plan to vote for Anderson.
Required:
a. What is the probability of this result (i.e. 144 voters or less out of 250) happening by chance, assuming the aggregate poll model proportion of 60% is correct?
b. Does your result from part I indicate that the number of voters who plan to vote for Anderson has decreased? In other words, is this outcome unusual?(Recall that an unusual event has a probability of 0.05 or less of occurring )
Answer:
a
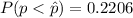
b
It is not an unusual event
Explanation:
From the question we are told that
The population proportion is p = 0.60
The sample size is n = 250
The number that plans to vote for Anderson is k = 144
Generally the mean of the sampling distribution is
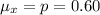
Generally the standard deviation is
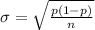
=>
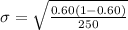
=>
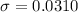
Generally the sample proportion is mathematically represented as
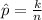
=>

=>

Gnerally the probability of this result (i.e. 144 voters or less out of 250) happening by chance, assuming the aggregate poll model proportion of 60% is correct is mathematically represented as
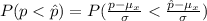
=>
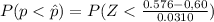
=>
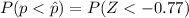
From the z-table the probability of (Z < -0.77) is
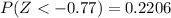
So
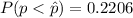
Since
 it implies that it is not an unusual event
it implies that it is not an unusual event