Question

A 126 N force is applied at an angle of 25.00 to a 8.50 kg block pressed against a rough vertical wall and the block slides down the wall at constant velocity. Calculate the coefficient of kinetic friction between the block and the wall.

Answer 1

μk = 0.58

Step-by-step explanation:

• If the block is sliding down at constant speed, this means that no net force is acting upon it in the vertical direction.
• As the block is pressed on the wall, this means that it doesnt accelerate in the horizontal direction either, so no net force acts upon it in this direction also.
• In this direction, we have only two forces acting, equal and opposite each other, one is the normal force (exerted by the wall) and the other is the horizontal component of the applied force.
• If the applied force forms an angle of 25º with the wall (which is vertical), this means that we can get its projection along the horizontal direction, using simple trigonometry , as follows:

`F_(apph) = F_(app) * sin\theta = 126 N * sin 25 = 53.3 N`

⇒
`F_(n) = - F_(apph) = -53.3 N`

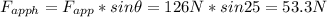
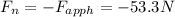
• In the vertical direction, we have three forces acting on the block: the weight pointing downward, the kinetic friction force (as we know that the block is sliding), and the vertical component of the applied force, in the same direction as the friction one.
• As we have already said, the sum of these forces must be 0.
  `F_(g) + F_(appv) + F_(ff) = 0 (1)`
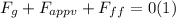
• where Fg is the weight of the block, Fappv is the vertical component of the applied force, and Fff is the kinetic friction force.
• Replacing these forces by their mathematical expressions, we have:

`F_(g) = m_(b) * g = 8.5 Kg * (-9.8 m/s2) = -83.3 N`

`F_(appv) = F_(app)* cos\theta = 126 N * cos 25 = 114.2 N`

`F_(ff) = \mu_(k)* F_(n) =\mu_(k) * (-53.3 N)`

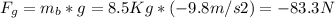
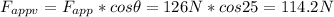
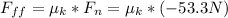
• Replacing in (1), and solving for μk, we finally get:

μk = 0.58