Answer:
The coordinates of the focus are
 anf the equation of the directrix is
anf the equation of the directrix is
 , respectively.
, respectively.
Explanation:
Let be
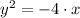 , which represents a parabola with a horizontal axis of symmetry. To find the location of the focus and to determine the equation of the directrix we must find the distance between focus and vertex (
, which represents a parabola with a horizontal axis of symmetry. To find the location of the focus and to determine the equation of the directrix we must find the distance between focus and vertex (
 ), dimensionless, a value than can be extracted from the following definition:
), dimensionless, a value than can be extracted from the following definition:
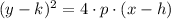 (Eq. 1)
(Eq. 1)
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 ,
,
 - Coordinates of the vertex, dimensionless.
- Coordinates of the vertex, dimensionless.
By direct comparison, we get the following coincidences:

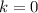
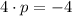 (Eq. 2)
(Eq. 2)
From (Eq. 2) we get that distance between focus and vertex is:
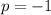
Which is consistent with the fact parabola has an absolute maximum.
Now, the location of the focus is:
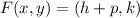 (Eq. 3)
(Eq. 3)
If know that
 ,
,
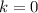 and
and
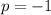 , coordinates of the focus is:
, coordinates of the focus is:
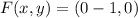

And the equation of the directrix is represented by:
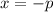 (Eq. 4)
(Eq. 4)
(
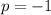 )
)

The coordinates of the focus are
 anf the equation of the directrix is
anf the equation of the directrix is
 , respectively.
, respectively.