Question

A DVD rental store wants to know what proportion of its customers are under age 21. A simple random sample of 400 customers was taken, and 280 of them were under age 21. Presume that the true population proportion of customers under age 21 is 0.68. What is the probability that the sample proportion \hat{p} is within 0.03 of the true proportion of customers who are under age 21 that is , what is the probability that \hat{p} is between 0.68 - 0.03 and 0.68 0.03

Answer 1

The sample proportion
`\hat{p}` is within 0.03 of the true proportion of customers who are under age 21 is 0.803

Explanation:

Total no. of customers = n = 400

We are given that the true population proportion of customers under age 21 is 0.68.

So, p =0.68

q=1-p=1-0.68=0.32

Standard deviation =
`\sqrt{(pq)/(n)}=\sqrt{(0.68 * 0.32)/(400)}= 0.023`

We are supposed to find the probability that the sample proportion
`\hat{p}` is within 0.03 of the true proportion of customers who are under age 21 that is , what is the probability that
`\hat{p}`is between 0.68 - 0.03 and 0.68+ 0.03

`P(0.65 < X < 0.71) = P(((0.65-0.68)/(0.0233)) < Z < ((0.71-0.68)/(0.0233)))`

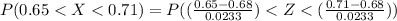
Using Z table

`= P(-1.2875 < Z < 1.2875)= 0.803`

Hence the sample proportion
`\hat{p}` is within 0.03 of the true proportion of customers who are under age 21 is 0.803