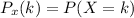Question

In Evans history class, 10 out of 100 key terms will be randomly selected to appear on the final exam; Evan must then choose 7 of those 10 to define. Since he knows the format of the exam in advance, Evan is trying to decide how many key terms he should study. (a) Suppose that Evan decides to study s key terms, where s is an integer between 0 and 100. Let X be the number of key terms appearing on the exam that he has studied. What is the distribution of X? Give the name and parameters, in terms of s. (b) Calculate the probability that Evan knows at least 7 of the 10 key terms that appear on the exam, assuming that he studies s = 75 key term

Answer 1

(a) Hypergeometric distribution

(b) 0.785384...

Explanation:

(a) looking at the question, we see that
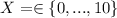`X = \in \{0, ... , 10 \}`, suppose Evans studied s key terms, this implies that he has not studied 100 - s key terms. Suppose
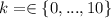`k = \in \{0, ... , 10 \}` if X = k, then k out of the s key terms he had studied appeared. But 10 - k out of 100 - s key terms he hasn't studied appeared. Thus X is an Hypergeometric distribution, X~HGeom(s, 100 - s, 10) with PMF:

`P_(x)(k) = P(X = k)`