Question

The population of weights of a particular fruit is normally distributed, with a mean of 464 grams and a standard deviation of 6 grams. If 27 fruits are picked at random, then 2% of the time, their mean weight will be greater than how many grams?

Answer 1

If 27 fruits are picked at random, then 2% of the time, their mean weight will be greater than 466.37 grams

Explanation:

Mean =
`\mu = 464`

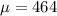
Standard deviation =
`\sigma = 6`

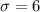
We are supposed to find If 27 fruits are picked at random, then 2% of the time, their mean weight will be greater than how many grams i.e.P(X>x)=0.02

The mean weight is in the highest 2%, you want to go to a z-table and find the z-score that where the area to the left of the curve is closest to 0.98.

n = 27

Refer the z -table

P(Z>x)=2.06

`(x-\mu)/((\sigma)/(√(n)))=2.06\\(x-464)/((6)/(√(27)))=2.06\\x-464=2.06 * (6)/(√(27))\\x=(2.06 * (6)/(√(27)))+464\\x=466.37`

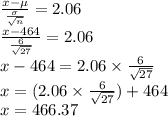
So, If 27 fruits are picked at random, then 2% of the time, their mean weight will be greater than 466.37 grams