Question

A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 444.0 gram setting. It is believed that the machine is underfilling the bags. A 40 bag sample had a mean of 443.0 grams. A level of significance of 0.02 will be used.

Required:
State the hypotheses. Assume the standard deviation is known to be 23.0.

Answer 1

Null hypothesis:

`\mathbf{H_o: \mu = 444}`

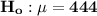
Alternative hypothesis:

`\mathbf{H_1: \mu < 444}`

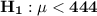
Explanation:

From the given information:

the population mean = 444

the sample mean = 443

number of samples = 40

standard deviation = 23

The null hypotheses and he alternative hypotheses can be computed as:

Null hypothesis:

`\mathbf{H_o: \mu = 444}`

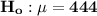
Alternative hypothesis:

`\mathbf{H_1: \mu < 444}`

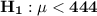
Thus, this is left-tailed since the alternative hypothesis is less than the population mean

The test statistics can be computed as follows:

`Z = (\overline x - \mu )/((\sigma)/(√(n)))`

`Z = (443 - 444 )/((23)/(√(40)))`

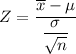
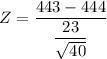
Z = - 0.275

At the level of significance of 0.02;

the critical value of
`Z_(\alpha/2) = Z_(0.02/2)=-2.05`

Decision rule: To reject the null hypothesis if the value of the Z score is lesser than the critical value.

Conclusion:

We fail to reject the null hypothesis and we conclude that sufficient evidence to support the claim that the machine bags were underfilled.