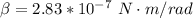Complete Question
Consider a 50-turn circular loop with a radius of 1.55 cm in a 0.35-T magnetic field. This coil is going to be used in a galvanometer that reads 45 μA for a full-scale deflection. Such devices use spiral springs which obey an angular form of Hooke's law, where the restoring torque is:
τs = -κ θ.
Here κ is the torque constant and θ is the angular displacement, in radians, of the spiral spring from equilibrium, where the magnetic field and the normal to the loop are parallel.
Required:
a. Calculate the maximum torque, in newton meters, on the loop when the full-scale current flows in it.
b. What is the torque constant of the spring, in newton meters per radian, that must be used in this device? Assume the full scale deflection is 60° from the spring's equilibrium position
Answer:
a
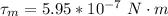
b
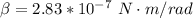
Step-by-step explanation:
From the question we are told that
The number of turns is N = 50
The radius is r = 1.55 cm = 0.0155 m
The magnetic field is B = 0.35 T
The induced current is
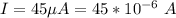
Generally the area of loop is mathematically represented as
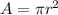
=>
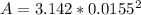
=>

Generally the maximum torque is mathematically represented as
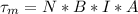
=>
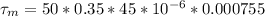
=>
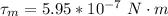
Generally the torque 60° from the spring's equilibrium position is mathematically represented as
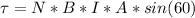
=>
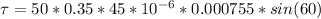
=>
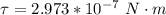
Generally the toque constant of the spring is mathematically represented as
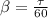
=>
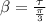
=>
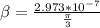
=>