Question

Find all relative extrema and classify each as a maximum or minimum. Use the second-derivative test where possible. f(x) = 125x 3 − 15x + 8

Answer 1

The following classification is found:

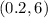`(0.2, 6)` - Absolute minimum

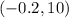`(-0.2, 10)` - Absolute maximum

Explanation:

Let be
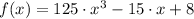`f(x) = 125\cdot x^(3)-15\cdot x + 8`, we need to find first and second derivatives of this expression at first:

First derivative

`f'(x) = 375\cdot x^(2)-15` (Eq. 1)

Second derivative

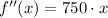`f''(x) = 750\cdot x` (Eq. 2)

Critical points are points that equals first derivative to zero and that may be maxima or minima. That is:

`375\cdot x^(2) -15 = 0`

`x = \pm \sqrt{(15)/(375) }`

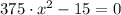
Which leads to the following critical points:

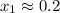`x_(1)\approx 0.2` and
`x_(2) \approx -0.2`

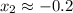
Now we evaluate each result in second derivative expression:

`f''(x_(1)) = 750\cdot (0.2)`

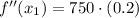
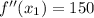`f''(x_(1))=150` (Absolute minimum)

`f''(x_(2))= 750\cdot (-0.2)`

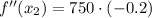
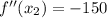`f''(x_(2)) = -150` (Absolute maximum)

Lastly we evaluate the function at each critical point:

`f(x_(1))= 125\cdot (0.2)^(3)-15\cdot (0.2)+8`

`f(x_(1))= 6`

`f(x_(2))= 125\cdot (-0.2)^(3)-15\cdot (-0.2)+8`

`f(x_(2)) = 10`

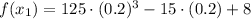
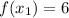
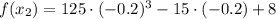
And the following classification is found:

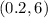`(0.2, 6)` - Absolute minimum

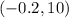`(-0.2, 10)` - Absolute maximum