Question

When a car's starter is in use, it draws a large current. The car's lights draw much less current. As a certain car is starting, the current through the battery is 64.2 A and the potential difference across the battery terminals is 9.36 V. When only the car's lights are used, the current through the battery is 1.96 A and the terminal potential difference is 11.3 V.

A. Find the battery's EMF.
B. What is its internal resistance?

Answer 1

EMF = 11.35 V

R = 0.031Ω

Step-by-step explanation:

To find the battery's EMF and the internal resistance we need to use Ohm's law:

`V = IR`

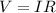
Where:

V: is the voltage

I: is the current

R is the resistance

We have:

The current through the battery is 64.2 A and the potential difference across the battery terminals is 9.36 V:

`\epsilon = V + IR`

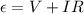
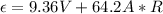`\epsilon = 9.36 V + 64.2A*R` (1)

When only the car's lights are used, the current through the battery is 1.96 A and the terminal potential difference is 11.3 V:

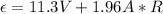`\epsilon = 11.3 V + 1.96A*R` (2)

By solving equation (1) and (2) for R we have:

`9.36 V + 64.2A*R = 11.3 V + 1.96A*R`

`R = (1.94 V)/(62.24A) = 0.031 \Omega`

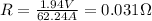
Hence, the internal resistance is 0.031 Ω.

Now, by entering R into equation (1) we can find the battery's EMF:

`\epsilon = 9.36 V + 64.2A*0.031 \Omega`

`\epsilon = 11.35 V`

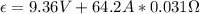
Therefore, the battery's EMF is 11.35 V.

I hope it helps you!