Question

Question Help When purchasing bulk orders of​ batteries, a toy manufacturer uses this acceptance sampling​ plan: Randomly select and test 36 batteries and determine whether each is within specifications. The entire shipment is accepted if at most 2 batteries do not meet specifications. A shipment contains 3000 ​batteries, and 3​% of them do not meet specifications. What is the probability that this whole shipment will be​ accepted? Will almost all such shipments be​ accepted, or will many be​ rejected?

Answer 1

The probability is
`P(X  \le 2 ) = 0.9072`

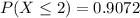
The company will accept 90.72% of the shipment and will reject
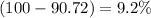`(100 -90.72) =  9.2\%` of the shipment , so many of the shipment are rejected

Explanation:

From the question we are told that

The sample size is n = 36

The proportion that did not meet the requirement is
`p =  0.03`

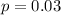
Generally the probability that the whole shipment is accepted is equivalent to the probability that there is at most 2 batteries that do not meet the requirement , this is mathematically represented as

`P(X  \le 2 ) = [ P(X =  0 ) +  P(X =  1 ) + P(X = 0)]`

=>
`P(X  \le 2 ) = [ [^(n)C_0 * (p)^(0) *(1-p)^(n-0) ] +  [^(n)C_1 * (p)^(1) *(1-p)^(n-1) ] +  [^(n)C_2 * (p)^(2) *(1-p)^(n-2) ]]`

Here C stands for Combination (so we will be making the combination function in our calculators )

So

=>
`P(X  \le 2 ) = [ [^(36)C_0 * (0.03)^(0) *(1-0.03)^(36-0) ] +  [^(36)C_1 * (0.03)^(1) *(1-0.03)^(36-1) ] +  [^(36)C_2 * (0.03)^(2) *(1-0.03)^(36-2) ]]`

=>
`P(X  \le 2 ) = [ [1 * 1 * 0.3340  ] +  [36* 0.03 *0.3444 ] +  [630 * 0.0009 *(0.355 ]]`

=>
`P(X  \le 2 ) = 0.9072`

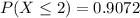
The company will accept 90.72% of the shipment and will reject
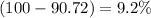`(100 -90.72) =  9.2\%` of the shipment , so many of the shipment are rejected