Question

4. According to Newton’s law of cooling, if an object at temperature T is immersed in a medium having the constant temperature M, then the rate of change of T is proportional to the difference of temperature M − T. This gives the differential equation dT dt = k(M − T). (a) Solve the differential equation for T. (b) A thermometer reading 100◦F is placed in a medium having a constant temperature of 70◦F. After 6 min, the thermometer reads 80◦F. What is the reading after 20 min?

Answer 1

a) The solution of the differential equation is
`T(t) = M + (T_(o)-M) \cdot e^{-(t)/(\tau) }`.

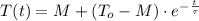b) The reading after 20 minutes is approximately 70.770 ºF.

Step-by-step explanation:

a) Newton's law of cooling is represented by the following ordinary differential equation:

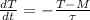`(dT)/(dt) = -(T-M)/(\tau)` (Eq. 1)

Where:

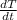`(dT)/(dt)` - Rate of change of temperature of the object in time, measured in Fahrenheit per minute.

`\tau` - Time constant, measured in minutes.

`T` - Temperature of the object, measured in Fahrenheit.

`M` - Medium temperature, measured in Fahrenheit.

Now we proceed to solve the differential equation:

`(dT)/(T-M) = -(t)/(\tau)`

`\int {(dT)/(T-M) } = -(1)/(\tau) \int \, dt`

`\ln (T-M) = -(t)/(\tau) + C`

`T(t) -M = (T_(o)-M)\cdot e^{-(t)/(\tau) }`

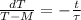
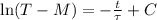
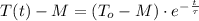
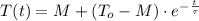`T(t) = M + (T_(o)-M) \cdot e^{-(t)/(\tau) }` (Eq. 2)

Where:

`t` -Time, measured in minutes.

`T_(o)` - Initial temperature of the object, measured in Fahrenheit.

b) From (Eq. 2) we obtain the time constant of the cooling equation for the object: (
`M = 70\,^(\circ)F`,
`T_(o) = 100\,^(\circ)F`,
`t = 6\,min`,
`T(t) = 80\,^(\circ)F`)

`80\,^(\circ)F = 70\,^(\circ)F + (100\,^(\circ)F-70\,^(\circ)F)\cdot e^{-(6\,min)/(\tau) }`

`e^{-(6\,min)/(\tau) } = (80\,^(\circ)F-70\,^(\circ)F)/(100\,^(\circ)F-70\,^(\circ)F)`

`e^{-(6\,min)/(\tau) } = (1)/(3)`

`-(6\,min)/(\tau) = \ln (1)/(3)`

`\tau = -(6\,min)/(\ln (1)/(3) )`

`\tau = 5.461\,min`

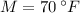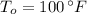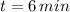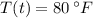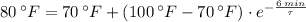
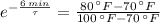
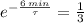
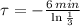
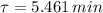
The cooling equation of the object is
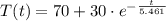`T(t) = 70 +30\cdot e^{-(t)/(5.461) }` and the temperature of the object after 20 minutes is:

`T(20) = 70+30\cdot e^{-(20)/(5.461) }`

`T(20) \approx 70.770\,^(\circ)F`

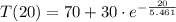
The reading after 20 minutes is approximately 70.770 ºF.