Answer:
a) According to the maximum-shear-stress failure theory, the static factor of safety of the shaft is 2.440.
b) According to the distortion-energy failure theory, the static factor of safety of the shaft is 2.816.
Step-by-step explanation:
First, we need to determine the torque experimented by the shaft (
 ), measured in kilonewton-meters, whose formula is described:
), measured in kilonewton-meters, whose formula is described:
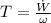 (Eq. 1)
(Eq. 1)
Where:
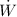 - Power, measured in kilowatts.
- Power, measured in kilowatts.
 - Angular velocity, measured in radians per second.
- Angular velocity, measured in radians per second.
If we know that
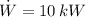 and
and
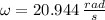 , then the torque experimented by the shaft:
, then the torque experimented by the shaft:
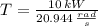
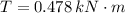
Let consider that shaft has a circular form, such that shear stress is determined by the following formula:
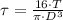 (Eq. 2)
(Eq. 2)
Where:
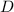 - Diameter of the shaft, measured in meters.
- Diameter of the shaft, measured in meters.
 - Torsional shear stress, measured in kilopascals.
- Torsional shear stress, measured in kilopascals.
If we know that
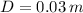 and
and
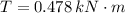 , the torsional shear stress is:
, the torsional shear stress is:
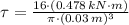
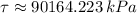
a) According to the maximum-shear-stress failure theory, we get that maximum shear stress limit is:
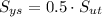 (Eq. 3)
(Eq. 3)
Where:
 - Ultimate shear stress, measured in kilopascals.
- Ultimate shear stress, measured in kilopascals.
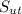 - Ultimate tensile stress, measured in kilopascals.
- Ultimate tensile stress, measured in kilopascals.
If we know that
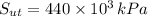 , the ultimate shear stress of the material is:
, the ultimate shear stress of the material is:
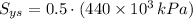
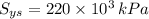
Lastly, the static factor of safety of the shaft (
 ), dimensionless, is:
), dimensionless, is:
 (Eq. 4)
(Eq. 4)
If we know that
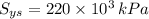 and
and
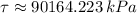 , the static factor of safety of the shaft is:
, the static factor of safety of the shaft is:

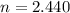
According to the maximum-shear-stress failure theory, the static factor of safety of the shaft is 2.440.
b) According to the distortion-energy failure theory, we get that maximum shear stress limit is:
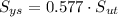 (Eq. 5)
(Eq. 5)
If we know that
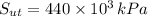 , the ultimate shear stress of the material is:
, the ultimate shear stress of the material is:
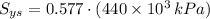

Lastly, the static factor of safety of the shaft is:
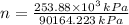

According to the distortion-energy failure theory, the static factor of safety of the shaft is 2.816.