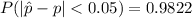Question

Suppose 52% of the population has a college degree. If a random sample of size 563563 is selected, what is the probability that the proportion of persons with a college degree will differ from the population proportion by less than 5%5%? Round your answer to four decimal places.

Answer 1

The value is
`P(| \^ p -  p| < 0.05 ) = 0.9822`

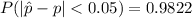
Explanation:

From the question we are told that

The population proportion is
`p =  0.52`

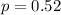
The sample size is n = 563

Generally the population mean of the sampling distribution is mathematically represented as

`\mu_(x) =  p =  0.52`

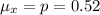
Generally the standard deviation of the sampling distribution is mathematically evaluated as

`\sigma  =  \sqrt{( p(1- p))/(n) }`

=>
`\sigma  =  \sqrt{( 0.52 (1- 0.52 ))/(563) }`

=>
`\sigma  =   0.02106`

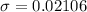
Generally the probability that the proportion of persons with a college degree will differ from the population proportion by less than 5% is mathematically represented as

`P(| \^ p -  p| < 0.05 ) =  P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 ))`

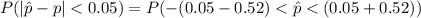
Here
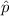`\^ p` is the sample proportion of persons with a college degree.

So

`P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 )) = P(([[0.05 -0.52]]- 0.52)/(0.02106) < ([\^p - p] - p)/(\sigma )  < ([[0.05 -0.52]] + 0.52)/(0.02106) )`

Here

`([\^p - p] - p)/(\sigma )  = Z (The\ standardized \  value \  of\  (\^ p - p))`

=>
`P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 )) = P[(-0.47 - 0.52)/(0.02106 )  <  Z  < (-0.47 + 0.52)/(0.02106 )]`

=>
`P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 )) = P[ -2.37 <  Z  < 2.37 ]`

=>
`P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 )) = P(Z <  2.37 ) - P(Z < -2.37 )`

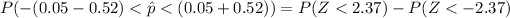
From the z-table the probability of (Z < 2.37 ) and (Z < -2.37 ) is

`P(Z <  2.37 ) = 0.9911`

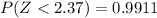
and

`P(Z <  - 2.37 ) = 0.0089`

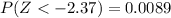
So

=>
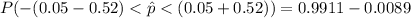
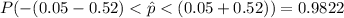
`P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 )) =0.9911-0.0089`

=>
`P( - (0.05 - 0.52 ) <  \^ p <  (0.05 + 0.52 )) = 0.9822`

=>
`P(| \^ p -  p| < 0.05 ) = 0.9822`