Question

Assume that silver and gold form ideal, random mixtures. Calculate the mass of pure Ag needed to cause an entropy increase of 20 J/K when mixed with 100g of pure Au

Answer 1

`m_(Ag)=2,265.9g`

Step-by-step explanation:

Hello!

In this case, since the definition of entropy in a random mixture is:

`\Delta S=-n_TR\Sigma[x_i*ln(x_i)]`

For this silver-gold mixture we write:

`\Delta S=-(n_(Au)+n_(Ag))R\Sigma[(n_(Au))/(n_(Au)+n_(Ag)) *ln((n_(Au))/(n_(Au)+n_(Ag)) )+(n_(Ag))/(n_(Au)+n_(Ag)) *ln((n_(Ag))/(n_(Au)+n_(Ag)) )]`

By knowing the moles of gold:

`n_(Au)=100g*(1mol)/(197g) =0.508mol`

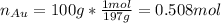
It is possible to write the aforementioned formula in terms of the variable
`x` representing the moles of silver:

`20(J)/(mol)=-(0.508+x)8.314(J)/(mol*K) \Sigma[(0.508)/(0.508+x) *ln((0.508)/(0.508+x) )+(x)/(0.508+x) *ln((x)/(0.508+x) )]`

Which can be solved via Newton-Raphson or a solver software, in this case, I will provide you the answer:

`x=n_(Ag)=21.0molAg`

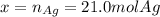
So the mass is:

`m_(Ag)=21.0mol*(107.9g)/(1mol)\\ \\m_(Ag)=2,265.9g`

Best regards!